מבחן מימד - בעיות הסתברות

הסתברות היא ביטוי מספרי לסיכוי שמאורע מסוים יקרה. כדי לחשב מה ההסתברות שיקרה מאורע, נחלק את מספר האפשרויות המתאימות לנו בסך כל האפשרויות הקיימות.

לדוגמה, אם אנו רוצים לדעת מה ההסתברות שיצא פלי (הצד עם המספר) בהטלת מטבע הוגן, נחלק את מספר האפשרויות שאותן אנו מחפשים (אפשרות אחת שיצא פלי) במספר האפשרויות הכולל של תוצאות בהטלת מטבע (שתי אפשרויות – עץ או פלי). מכאן, ההסתברות שייצא פלי בהטלת מטבע היא 1/2 . נשתמש לעתים בשיעור זה במושג "מאורע". "מאורע" הוא מצב שניתן לייחס לו הסתברות.

 

כלל: הסתברות נעה רק בין 0 ל- 1. הסתברות 0 אומרת שאין סיכוי שהדבר יקרה. הסתברות 1 אומרת שהדבר יקרה בוודאות.

לדוגמה: בשק 3 כדורים כחולים. ההסתברות להוציא מהשק כדור ירוק היא 0. זאת מכיוון שבשק אין כדור ירוק (יש רק כדורים כחולים), ולכן האפשרות של הוצאת כדור ירוק לא יכולה להתרחש - .

ההסתברות שבהוצאת כדור מן השק נוציא כדור כחול היא 1, זאת מכיוון שבשק יש רק כדורים כחולים וכל כדור שנוציא בוודאות יהיה כחול -  .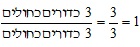

בשאלות מסוג "או" אנו נשאלים מה ההסתברות שיקרה מאורע אחד או מאורע אחר. בשאלות "או" נסכום את ההסתברות למאורע הראשון עם ההסתברות למאורע השני. תוצאת הסכום תהיה ההסתברות שיקרה המאורע הראשון או שיקרה המאורע השני.

לדוגמה, בשק 3 כדורים בצבעים ירוק, כחול ואדום. מה ההסתברות שבהוצאת כדור מן השק נוציא כדור ירוק או כחול?

בסך הכול יש 3 אפשרויות להוצאת כדור מן השק (ירוק, כחול ואדום). נחשב את ההסתברות להוצאת כדור כחול – מקרה אחד מתוך 3 אפשרויות - כלומר 1/3.

ההסתברות להוצאת כדור ירוק מן השק היא 1/3. לכן, ההסתברות להוצאת כדור ירוק או כדור כחול היא 2/3=1/3+1/3. 

בשאלות מסוג "וגם" אנו נשאלים מה ההסתברות שיקרה מאורע אחד וגם מאורע אחר. בשאלות "וגם" נכפול את ההסתברות למאורע הראשון בהסתברות למאורע השני. תוצאת המכפלה תהיה ההסתברות שיקרה המאורע הראשון וגם שיקרה המאורע השני.

לדוגמה, בשק 3 כדורים בצבעים ירוק, כחול ואדום. מה ההסתברות שבהוצאת 2 כדורים מן השק נוציא תחילה כדור ירוק ולאחר מכן כדור כחול (לאחר כל הוצאת כדור הוא מוחזר לשק)?

בסך הכול יש 3 אפשרויות להוצאת כדור מן השק (ירוק, כחול ואדום). נחשב את ההסתברות להוצאת כדור ירוק – מקרה אחד מתוך 3 אפשרויות, כלומר 1/3. בדרך דומה, גם ההסתברות להוצאת כדור כחול מן השק היא 1/3. מכאן ההסתברות להוצאת כדור ירוק ולאחר מכן כדור כחול היא 1/9=1/3*1/3.

שימו לב: אם השאלה לא הייתה מגדירה את סדר ההוצאות, כלומר לא היה משנה אם היינו מוציאים קודם כדור כחול ואחר כך ירוק או להיפך (כלומר היינו נשאלים רק מה הסיכוי שנוציא כדור כחול וגם כדור ירוק), ההסתברות הייתה גדלה פי 2. זאת מכיוון שההסתברות להוצאת כדור כחול ואחר כך ירוק היא 1/9, וההסתברות להוצאת כדור ירוק ואחר כך כדור כחול גם היא שווה ל- 1/9; מכיוון ששתי האפשרויות מקיימות את הנדרש בשאלה, יש ביניהן "או"; או שנוציא קודם כדור כחול ואז ירוק, או שנוציא קודם כדור ירוק ואז כחול, ושני המקרים מתאימים לנו. לכן נסכום את שתי ההסתברויות ונקבל 2/9=1/9+1/9.

מאורע משלים של אירוע x הוא מאורע שבו x לא יקרה.
לדוגמה, המאורע המשלים שייצא פלי בהטלת מטבע, הוא שייצא עץ. זאת מכיוון שיש רק 2 אפשרויות של תוצאה: עץ ופלי, ואם לא יצא פלי, בוודאות יצא עץ.

כלל: סכום ההסתברויות של מאורע והמאורע המשלים לו בהכרח שווה ל- 1.

לדוגמה: אם ההסתברות שיירד גשם ביום מסוים היא 0.3, המאורע שלא יירד גשם הוא המאורע המשלים וסכום שתי ההסתברויות של "יירד גשם" ו"לא יירד גשם" חייב להיות שווה ל- 1. מכאן ההסתברות שלא יירד גשם שווה ל- 0.7=1-0.3. במקרים אחדים יהיה לנו קל יותר לחשב את ההסתברות שיקרה המאורע המשלים ולחסר את ההסתברות שמצאנו מ- 1 על מנת למצוא את ההסתברות שיתרחש מאורע כלשהו.

לדוגמה, יוסי זורק כדור לסל 4 פעמים. בכל פעם ההסתברות שלו לקלוע היא 0.5. מה הסיכוי שיוסי יקלע לסל לפחות פעם אחת?

כדי לחשב את ההסתברות שיוסי יקלע לסל לפחות פעם אחת, עלינו לחשב את ההסתברות שיוסי יקלע לסל פעם אחת, ועוד ההסתברות שיוסי יקלע לסל פעמיים, ועוד ההסתברות שיוסי יקלע לסל שלוש פעמים ועוד ההסתברות שיוסי יקלע לסל ארבע פעמים. קשה לחשב ולסכום את כל ההסתברויות, ולכן נחשב תחילה מה הסיכוי של המאורע המשלים ולאחר מכן נחסר את התוצאה מ- 1. המאורע המשלים לקליעה אחת לפחות הוא לא לקלוע כלל. הסיכוי שיוסי לא יקלע כלל הוא הסיכוי שהוא לא יקלע בפעם הראשונה וגם השנייה וגם השלישית וגם הרביעית. הסיכוי שהוא לא יקלע עבור כל אחת מהפעמים הוא 1/2 (הוא שווה ל- 1 פחות ההסתברות לקלוע, שנתונה ושווה ל- 1/2). כלומר, ההסתברות שיוסי לא יקלע בכל 4 הזריקות היא 

1/16=1/2*1/2*1/2*1/2. מכאן ההסתברות שיוסי יקלע פעם אחת לפחות היא 15/16=1/16- 1.