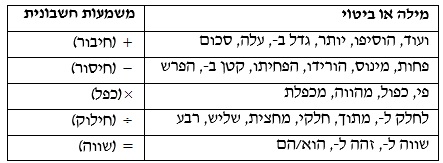
- ממוצע חשבוני של קבוצת ערכים הינו סכום האיברים המשתתפים בו, חלקי מספר האיברים.
- ממוצע של קבוצת איברים שאינם זהים זה לזה, יהיה תמיד בתחום שבין האיבר הגדול ביותר לאיבר הקטן ביותר, באופן הבא: האיבר הגדול ביותר > ממוצע > האיבר הקטן ביותר.
- הממוצע לא יכול להיות גדול או שווה לאיבר הגדול ביותר בקבוצה.
- הממוצע לא יכול להיות קטן או שווה לאיבר הקטן ביותר בקבוצה.
- ממוצע של קבוצת איברים זהים זה לזה יהיה בדיוק כגודל האיברים.
- ממוצע משוקלל הוא ממוצע שבו מובא בחשבון משקלו היחסי של כל אחד מהערכים בקבוצה.
לדוגמה, נניח ואנו רוצים לחשב ממוצע בגרות משוקלל עבור מקצועות בגרות, וסה"כ יחידות לימוד: 5 יחידות בגרות במתמטיקה בציון 80
3 יחידות בגרות בגיאוגרפיה בציון 70
2 יחידות בגרות בתנ"ך בציון 60
הממוצע המשוקלל יחושב באופן הבא:
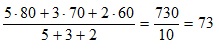
- סכום המרחקים של האיברים הגדולים מהממוצע שווה לסכום המרחקים של האיברים הקטנים מהממוצע.
- המרחק של האיבר שנוסף מהממוצע מתחלק על פני כל איברי הקבוצה (כולל הוא עצמו), והמנה שנקבל היא השינוי בממוצע.
- המרחק של האיבר שירד מהממוצע מתחלק על פני כל האיברים שנותרו בקבוצה, והמנה שנקבל היא השינוי בממוצע.
- ביצוע של אחת מארבע פעולות חשבון בסיסיות (חיבור/חיסור/כפל/חילוק) באופן רוחבי על קבוצת איברים מסוימת, יביא לשינוי זהה בממוצע לפי אותה פעולת חשבון.
- אם מספר האיברים בסדרה הוא אי-זוגי, הממוצע הוא האיבר האמצעי בגודלו.
- אם מספר האיברים בסדרה הוא זוגי, הממוצע הוא האמצע בין שני האיברים האמצעיים בגודלם.


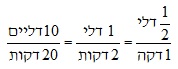 .
.