חשיבה כמותית במבחן הפסיכוטכני
הרמה המתמטית הנדרשת במבחן מקבילה לזו הנלמדת בכיתות ח'-ט', כך שרוב המועמדים לשירות ביטחון המגיעים ליום המיונים בגיל (כיתה י"א לכל הפחות) אמורים כבר להכיר את התכנים הרלוונטיים ולשלוט בהם. בנוסף, השאלות בפרק זה אמורות להיפתר באמצעות חישוב קצר אותו ניתן לבצע בפרק זמן של כדקה בממוצע, גם כאשר הוא מורכב ממספר שלבים.
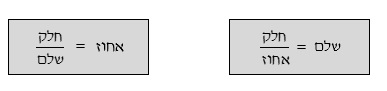
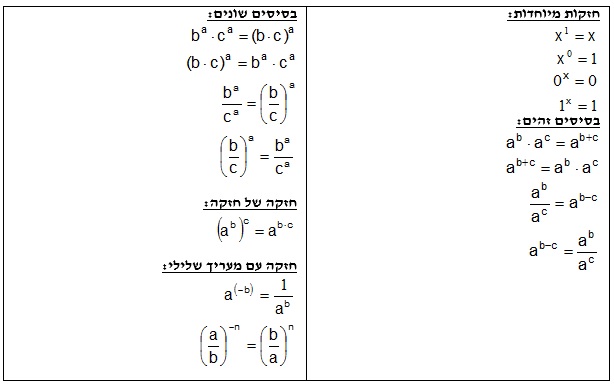
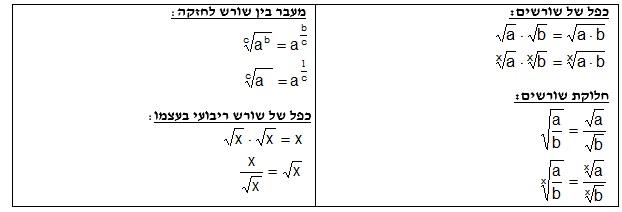
השאלות המופיעות בפרק החשיבה הכמותית במבחן עוסקות במגוון נושאים מתמטיים בסיסיים, ביניהם אחוזים, ממוצע, חזקות, שורשים, סדר פעולות חשבון, שברים, בעיות תנועה, בעיות הספק, יחס, בעיות כלליות ועוד. סוגי השאלות המופיעות בפרק מעורבבים, כאשר הניקוד שניתן לכל שאלה זהה. זכרו כי פתרון השאלות בכל הנושאים הכמותיים בבחינה אינו מצריך שימוש במחשבון או היכרות עם נוסחה מורכבת, כך שלאחר היכרות כללית עם הנושאים ניתן לפתור את השאלות במהירות יחסית.
השאלות המופיעות בפרק החשיבה הכמותית במבחן עוסקות במגוון נושאים מתמטיים בסיסיים, ביניהם אחוזים, ממוצע, חזקות, שורשים, סדר פעולות חשבון, שברים, בעיות תנועה, בעיות הספק, יחס, בעיות כלליות ועוד. סוגי השאלות המופיעות בפרק מעורבבים, כאשר הניקוד שניתן לכל שאלה זהה. זכרו כי פתרון השאלות בכל הנושאים הכמותיים בבחינה אינו מצריך שימוש במחשבון או היכרות עם נוסחה מורכבת, כך שלאחר היכרות כללית עם הנושאים ניתן לפתור את השאלות במהירות יחסית.

 .
.