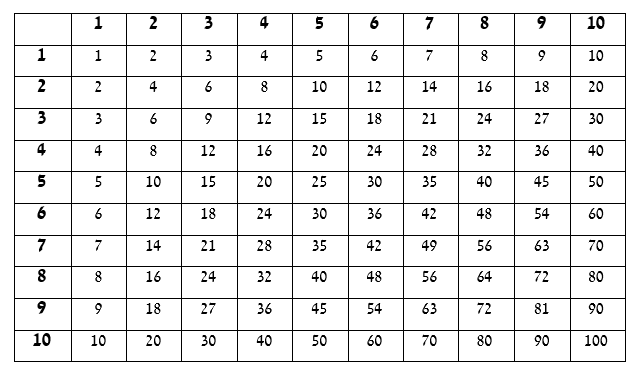
האחוז - %השלם, בין אם הוא בריכה אחת או 20 אנשים וכדומה, מהווה 100%. כך לדוגמה כיתה של 20 תלמידים מהווה 100 אחוז וחצי כיתה, 10 תלמידים, מהווה 50%. היות והשלם יכול להיות 20 תלמידים או עוגה אחת, תמיד נבדוק מהו השלם ולאחר מכן נתייחס לאחוז מתוך השלם. אל האחוז מתוך השלם ניתן להתייחס כאל שבר עם מכנה 100.
חישוב אחוזיםהשלם הוא 100 אחוז ו-1% מתוכו מהווה 1/100. לדוגמה, אם נרצה לתת טיפ של 10% מתוך חשבון על סך 100 שקלים, ניתן 10/100 (לאחר צמצום 1/10) מתוך השלם. כלומר, 10=100*1/10 (עשרה שקלים טיפ). אם החשבון היה על סך 250 שקלים, הנוסחה הייתה נראית כך 25=250*1/10 (25 שקלים טיפ).
כלל: כאשר נרצה לחשב גודל כלשהו של אחוז מהשלם, לדוגמא %x, נכפול את x ב- 1/100 ובשלם עצמו (למשל y), ונקבל את הגודל המבוקש מתוך השלם:
 אחוזים גדולים מ- 100%
אחוזים גדולים מ- 100%
ניתן לחשב אחוזים גדולים מ-100%, והדרך לחישובם זהה לחישוב הרגיל. לדוגמה, קרן קונה נעליים ב- 50 שקלים ומוכרת אותם ב-200% מהמחיר שבו היא קונה את הנעליים, אז קרן מוכרת את הנעליים ב-100=50*(1/100)*200 שקלים. מעבר לחישוב האלגברי, נוכל להבין שאם 50 שקלים הם 100%, אז 200% הם 200%=100%+100%, כלומר 100=50+50.
אחוזים שמומלץ לזכור בעל-פה

מציאת השלם
קיימות שאלות אחוזים בהן אנו נדרשים למצוא את השלם על סמך נתונים על אחוז מסוים ממנו. לדוגמה, 30% מתוך לקוחותיה של חברת "רותי ביוטי" הם גברים. נתון לנו שלחנות זו ישנם 60 לקוחות גברים. כמה לקוחות (גברים ונשים) יש לחנות "רותי ביוטי"? בשאלות מסוג זה נשתמש בנוסחה הבאה:
החלק הנתון = אחוז מתוך השלם * השלם
דרך ההצבה:אנו מחפשים את השלם ולכן נציב במקומו X. אחוז הגברים מתוך כלל לקוחות החנות נתון לנו והוא 30% לכן נציב זאת בצורת שבר(30/100). כמות הגברים, החלק הנתון, הוא 60, לכן המשוואה צריכה להיראות כך:
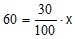
נבודד את X ונקבל
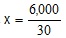
לאחר צמצום השבר נקבל X = 200 שזהו סך כל הלקוחות(נשים וגברים) של חנות "רותי ביוטי".
הצבת 100 בתור שלםקיימות שאלות אחוזים בהן לא נתונים לנו מספרים אלא אחוזים בלבד. ניתן לפתור שאלות אלה ע"י חישוב אלגברי, אך חישוב זה הוא ארוך ולעתים מסובך. אנו ממליצים לפתור שאלות אלה ע"י הצבת מספרים.
המספר הנוח ביותר להצבה הוא 100 מכיוון שכל אחוז מתוך 100 שווה בערכו לגודל האחוז. לדוגמה, 5% מתוך 100 הם 5, 10% מתוך 100 הם 10 וכן הלאה.
חישוב מהיר של 10%ישנם אחוזים שקל מאוד לחשב מתוך השלם. לדוגמה, 10% (1/10) ניתנים לחישוב מהיר ע"י חילוק השלם ב-10. כך, לדוגמה, נדע מיד כי 10% מתוך 20 הם 2 (20/10), 10% מתוך 240 הם 24 (240/10) וכן הלאה. בדרך דומה, נוכל לחשב כמה הם 10% גם ממספרים שאינם מתחלקים ב-10. לדוגמה, 10% מתוך 55 הם 5.5 (55/10).
ע"י חישוב מהיר של 10% מתוך השלם נוכל בקלות גם למצוא אחוזים אחרים. כלומר, אם 10%*3 = 30% אז נוכל לדעת בקלות מה ערכם של 30% מ- 55. בדוגמה שלמעלה מצאנו ש- 10% מ- 55 הם 5.5. מכאן 30% מ- 55 הם 16.5=5.5*3.